To get a concrete sense of this dynamic, ordering process in a complex adaptive system as it relates to COVID-19 in mid-21st Century health care systems, we return to a portrayal of complex adaptive systems that we introduced in our second essay in this series (Bergquist and Fish, 2023). This portrayal was first offered by a noted biologist, Conrad Waddington (1997) more than twenty years ago. He describes warped planes on which objects move in an unpredictable manner. Using the metaphor of a ball being placed at the top of a slopping plane (thin sheet of metal or plastic) that has been bent and warped (forming ridges and valleys) Waddington notes that the ball will begin to roll straight down the plane until it encounters one of the ridges. At this point a series of oscillations tend to occur. The ball moves back and forth before it eventually begins to roll down one of the valleys and picks up speed again.
Graph One: The Warped Plane
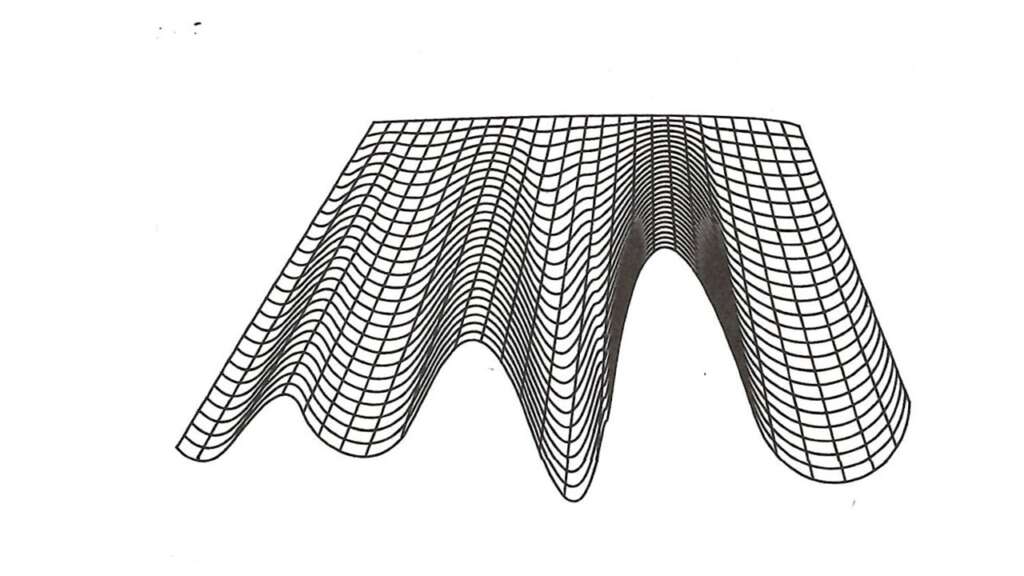If several balls are rolling down the plane at the same time, this first ridge will become a point of bifurcation for the entire system. Some balls will move in one direction (depending on the pattern of oscillation when encountering the ridge) and roll down one valley, while other balls will move in a different direction, rolling down one or more of the other valleys. A ball may gain enough momentum to roll over the top of one ridge into a second valley. If there is not sufficient momentum, the ball will remain in the current valley.
Thus, a few critical moments in the life of the ball’s roll down the plane make a major difference in the outcome of the roll. The pattern of oscillation determines which valley is chosen and whether or not the momentum is sufficient for the ball to shift to another valley. There is a cluster of conditions (in the form of valleys and ridges) that define the specific alternative courses to be taken by the ball.
